Übungsaufgabe zu: Kostenfunktion, Erlösfunktion, Gewinnfunktion und deren Zusammenhang im Polypol und Monopol
Ein Unternehmen bietet sein Produkt auf einem monopolistischen Markt an. Das Unternehmen muss auf dem Markt für das von ihm angebotene Produkt einen Höchstpreis von 49 GE/ME und eine Sättigungsmenge von 7 ME akzeptieren, wobei bei der Produktion von 7 ME nur noch ein Mindespreis von 0 GE/ME erzielt werden kann. Für das Unternehmen gilt eine ertragsgesetzliche Gesamtkostenfunktion. Die Fixkosten des Unternehmens betragen 32 GE. Bei einer Produktion von 4 ME hat das Unternehmen Kosten von 60 GE. Die Kapizitätsmenge entspricht bei diesem Unternehmen der Sättigungsgrenze. Hier entstehen die höchsten Produktionskosten mit 186 GE. Der degressive Kostenverlauf geht bei einer Produktion von 2 ME in einen progressiven Kostenverlauf über.
- Ermitteln Sie die Funktionsgleichung der
- Erlösfunktion
- Gesamtkostenfunktion
- Gewinnfunktion
- Bestimmen Sie bei welcher Menge der Erlös maximal ist und die Höhe des maximalen Erlöses.
- Bestimmen Sie die Gewinnschwelle (Break-even-Point) und die Gewinngrenze.
- Bestimmen Sie den Stückpreis auf dem Markt bei gewinnmaximaler Ausbringungsmenge (Cournot'scher Punkt). Berechnen Sie den maximalen Gewinn.
- Zeichne mit Geogebra alle ermittelten Funktionen und alle bestimmten Punkte bzw. Stellen in eine einzige Zeichnung und beschrifte diese Zeichnung aussagekräftig und übersichtlich.
Probiere es erst ohne jeglichen Hinweis. Herauskommen müsste folgendes:
- Funktionsgleichungen:
- Erlösfunktion: E(x) = -7x2 + 49x
- Gesamtkostenfunktion: K(x) = x3 - 6x2 + 15x + 32
- Gewinnfunktion: G(x) = -x3 - x2 + 34x - 32
-
Die Erlöse sind maximal bei 3,5 ME.
Emax = 85,75 GE. -
Gewinnschwelle bei 1 ME.
Gewinngrenze bei 4,74 ME. -
Gewinnmaximale Ausbringungsmenge: 3,05 ME
Gmax = 34,03 GE.
Stückpreis bei gewinnmaximaler Ausbringungsmenge: 27,65 GE/ME.
Cournot'scher Punkt: C(3,05 ME | 27,65 GE/ME)
Um die Erlösfunktion aufzustellen, muss zunächst analysiert werden, welche Hinweise zur Erlösfunktion in der
Aufgabenstellung enthalten sind.
Direkte Hinweise zur Erlösfunktion sind in Aufgabenstellung nicht enthalten, aber indirekte Hinweise.
Die Erlösfunktion erechnet sich aus der Preisfunktion: E(x) = p(x)·x. Hinweise zur Preisfunktion sind in der
Aufgabenstellung dirket enthalten.
Folgende Hinweise für die Preisfunktion sind in der Aufgabenstellung direkt enthalten:
a) Lösungshinweise zur Bestimmung der Erlösfunktion
Hinweis 1
Hinweis 2
Hinweis 3
Hinweis 4
Die Hinweise für die Preisfunktion können folgendermaßen mathematisiert werden:
Hinweis 5
Die Preisfunktion hat also die beiden Unbekannten a und b. Ferner sind zwei Bedingungen für die Preisfunktion
gegeben. D.h. es gibt genauso viele Unbekannte wie es Bedingungen gibt und es müsste eine eindeutige Lösung
für die Preisfunktion geben.
Hinweis 6
Mit der Bedingung p(0) = 49 ist b direkt gegeben, da ja gilt p(x)=ax+b --> p(0) = a·0 + b --> p(0) = b.
Hinweis 7
--> b = 49
p(x) = ax + 49
Es muss also nur noch a bestimmt werden.
Um a in p(x) = ax + 49 zu bestimmen, wird die zweite Bedingung p(7) = 0 benötigt.
Hinweis 8
Gegeben sind p(x) = ax + 49 und p(7) = 0
Hinweis 9
--> p(7) = a·7 + 49 = 0
--> 7a + 49 = 0
--> 7a = -49
--> a = -7
--> Preisfunktion: p(x) = -7x + 49
Jetzt kann die Erlösfunktion bestimmt werden.
Hinweis 10
Mit p(x) = -7x + 49 kann jetzt E(x) bestimmt werden:
Hinweis 11
E(x) = p(x)·x
E(x) = (-7x + 49)·x
Bemerkung: Die Klammer ist wichtig, da sonst Punkt- vor Strichrechnung gilt und nur 49 mit x multipliziert würde.
Erlösfunktion: E(x) = -7x2 + 49x
Um die Gesamtkostenfunktion aufzustellen, muss zunächst analysiert werden, welche Hinweise zur Gesamtkostenfunktion
in der Aufgabenstellung enthalten sind.
In der Aufgabenstellung sind folgende direkte Hinweise zur Gesamtkostenfunktion enthalten:
a) Lösungshinweise zur Bestimmung der Gesamtkostenfunktion
Hinweis 1
Hinweis 2
Hier entstehen die höchsten Produktionskosten mit 186 GE.
Die Hinweise für die Preisfunktion können folgendermaßen mathematisiert werden:
Hinweis 3
Hier entstehen die höchsten Produktionskosten mit 186 GE --> K(7) = 186
Die Gesamtkostenfunktion hat also die vier Unbekannten a, b, c und d. Ferner sind vier Bedingungen für die
Gesamtkostenfunktion gegeben. D.h. es gibt genauso viele Unbekannte wie es Bedingungen gibt und es müsste
eine eindeutige Lösung für die Gesamtkostenfunktion geben.
Hinweis 4
Mit K(x) = ax3 + bx2 + cx + d
Hinweis 5
und den vier Bedingungen:
(1) K(0) = 32
(2) K(4) = 60
(3) K(7) = 186
(4) K''(2) = 0
lässt sich jetzt ein lineares Gleichungssystem aufstellen, das sich dann mit Geogebra lösen lässt.
Aufstellen des linearen Gleichungssystems mit K(x) = ax3 + bx2 + cx + d
Hinweis 6
und den vier Bedingungen:
(1) K(0) = 32 --> a·03 + b·02 + c·0 + d = 32 --> d = 32
(2) K(4) = 60 --> a·43 + b·42 + c·4 + d = 60 --> 64a + 16b + 4c + d = 60
(3) K(7) = 186 --> a·73 + b·72 + c·7 + d = 60 --> 343a + 49b + 7c + d = 186
(4) K''(2) = 0 --> Hier muss zunächst die zweite Ableitungsfunktion berechnet werden:
Erste Ableitungsfunktion: K'(x) = 3ax2 + 2bx + c
Zweite Ableitungsfunktion: K''(x) = 6ax + 2b
Mit K''(2) = 0 folgt daraus:
K''(2) = 6a·2 + 2b = 0 --> 12a + 2b = 0
Da die erste Gleichung des Gleichungssystems d = 32 lautet, kann in den Gleichungen (2) - (4) zunächst einmal
d durch 32 ersetzt werden und dann die Gleichungen so umgestellt werden, dass auf der linken Seite jeweils nur
die Terme mit den Unbekannte a,b und c stehen:
Hinweis 7
(2) 64a + 16b + 4c + 32 = 60 --> 64a + 16b + 4c = 28
(3) 343a + 49b + 7c + 32 = 186 --> 343a + 49b + 7c = 154
(4) 12a + 2b = 0 (Bemerkung: Hier muss nichts weiter gemacht werden, da in dieser Gleichung kein d enthalten ist.)
Es wird jetzt also ein lineares Gleichungssystem mit 3 Gleichungen und den 3 Unbekannten a,b und c erhalten.
Diese drei Gleichungen können jetzt in Geogebra eingegeben werden, wobei man die Buchstaben a,b, und c durch x, y
un z ersetzen sollte, damit Geogebra a, b und c nicht für Parameter hält:
Hinweis 8
(2) 64a + 16b + 4c = 28 --> 64x + 16y + 4z = 28
(3) 343a + 49b + 7c = 154 --> 343x + 49y + 7z = 154
(4) 12a + 2b = 0 --> 12x + 2y = 0
Man muss die CAS-Ansicht in Geogebra einschalten. Nachdem dann die 3 Gleichungen in Geogebra eingegeben wurden,
müsste es folgendermaßen aussehen:
Hinweis 9
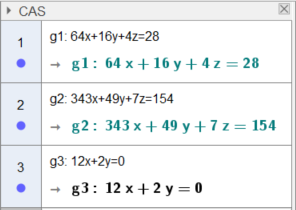
Wenn jetzt mit Hilfe der gedrückten Strg-Taste alle drei Gleichungen markiert werden und dann mit Hilfe
des Menüpunktes Lösen Hinweis 10
 das Gleichungssystem gelöst wird, dann
zeigt Geogebra folgendes an:
das Gleichungssystem gelöst wird, dann
zeigt Geogebra folgendes an:
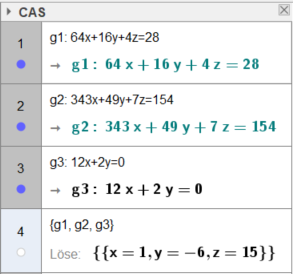
Als Lösung des Gleichungssystems berechnet Geogebra x = 1, y = -6 und z = 15. Da zuvor a, b und c durch x, y und z
ersetzt wurden, ergibt sich als Lösung des Gleichungssystems als a = 1, b = -6 und c = 15.
Hinweis 11
Mit a = 1, b = -6, c = 15 und d =32 ergibt sich nun die folgende Gesamtkostenfunktion:
Hinweis 12
K(x) = 1·x3 - 6·x2 + 15·x + 32
also
K(x) = x3 - 6x2 + 15x + 32
Um die Gewinnfunktion aufzustellen, muss zunächst analysiert werden, welche Hinweise zur Gewinnfunktion
in der Aufgabenstellung enthalten sind.
Zur Gewinnfunktion sind überhaupt keine direkten Hinweise enthalten. Es sind nur direkte Hinweise
zur Preisfunktion und damit indierekte Hinweise zur Erlösfunktion und direkte Hinweise zur Gesamtkostenfunktion
in der Aufgabenstellung enthalten. Es sind also nur sehr indirekt Hinweise zur Gewinnfunktion in der
Aufgabenstellung enthalten, da sich die Gewinnfunktion aus der Erlös- und der Gesamtkostenfunktion ergibt.
Deshalb müssen vor der Lösung dieser Aufgabenstellung erst die Erlösfunktion und die Gesamtkostenfunktion
bestimmt werden.
Für die Gewinnfunktion gilt formal: G(x) = E(x) - K(x)
Mit E(x) = -7x2 + 49x
G(x) = (-7x2 + 49x) - (x3 - 6x2 + 15x + 32)
a) Lösungshinweise zur Bestimmung der Gewinnfunktion
Hinweis 1
Hinweis 2
Hinweis 3
Hinweis 4
und
K(x) = x3 - 6x2 + 15x + 32
ergibt sich
G(x) = E(x) - K(x)
G(x) = (-7x2 + 49x) - (x3 - 6x2 + 15x + 32)
Bemerkung: Lieber erstmal Klammern um beide Ausdrücke für E(x) und K(x) machen, um zu verdeutlichen,
dass es sich hier ursprünglich um 2 Funktionen handelt.
Hinweis 5
Die erste Klammer kann einfach weggelassen werden, da kein Minuszeichen vor der Klammer steht. Bei der zweiten
Klammer ist dies anders. Vor dieser steht ein Minuszeichen. D.h. die Vorzeichen in der Klammer "drehen sich um".
G(x) = -7x2 + 49x - x3 + 6x2 - 15x - 32
Jetzt noch nach Potenzen ordnen:
G(x) = -x3 - 7x2 + 6x2 + 49x - 15x - 32
und zusammenfassen:
G(x) = -x3 - x2 + 34x - 32
Gewinnfunktion: G(x) = -x3 - x2 + 34x - 32
Es soll die Menge des maximalen Erlöses und der maximale Erlös selbst berechnet werden. Es wird also die
Erlösfunktion E(x) benötigt.
Da der maximale Erlös Emax und die zugehörige Menge bestimmt werden soll, muss zunächst die Maximumstelle
der Erlösfunktion berechnet werden.
Da bei der Maximumstelle einer Funktion f die Steigung des Graphen der Funktion 0 ist und die Steigung einer
Funktion an jeder Stelle durch die Funktionwerte der 1. Ableitungsfunktion f' dieser Funktion bestimmt ist, muss
die 1. Ableitungsfunktion E' der Erlösfunktion E bestimmt werden.
Bestimmung der 1. Ableitungsfunktion E' der Erlösfunktion E:
Bestimmung Maximumstelle von E, also der Stelle, an der die Steigung der Funktion gleich 0 ist:
Der Erlös ist maximal bei x = 3,5 ME. Jetzt muss noch der maximale Erlös Emax berechnet werden.
x = 3,5 ME muss in die Erlösfunktion eingesetzt werden, da diese ja zu jeder Menge x, die entsprechende Erlöse
als Funktionswerte hat.
Berechnung der maximalen Erlöses Emax:
b) Lösungshinweise zur Bestimmung des maximalen Erlöses und der zugehörigen Menge
Hinweis 1
Hinweis 2
Hinweis 3
Hinweis 4
E(x) = -7x2 + 49x
E'(x) = -14x + 49
Hinweis 5
E'(x) = 0
-14x + 49 = 0
-14x = -49
14x = 49
x =
x = 3,5
Bemerkung: Da der Graph der Erlösfunktion E(x) = -7x2 + 49x eine ganzrationale Funktion 2. Grades
und wegen des negativen Formfaktors a = -7 eine nach unten geöffnete Parabel ist, muss hier nicht mit
der 2. Ableitung der Funktion E überprüft werden, ob es sich bei x = 3,5 um eine Maximum- oder Minimumstelle
oder überhaupt um eine solche Stelle handelt (es könnte ja bei höhergradigen Funktionen auch ein Sattelpunkt
sein), sondern es muss sich bei einem solchen Verlauf um eine Maximumstelle handeln.
Der Erlös ist also bei einer Menge von x = 3,5 ME maximal.
Hinweis 6
In welche Funktion muss jetzt x = 3,5 ME eingesetzt werden.
Hinweis 7
Bemerkung: würde x = 3,5 in die erste Ableitungsfunktion E' eingesetzt, dann würde 0 herauskommen.
Mit dem Ansatz E'(x)=0 wurde ja die erlösmaximale Menge x = 3,5 durch Ustellen berechnet. Würde man also
x = 3,5 wieder in E'(x) einsetzen, wird nur die Probe gemacht, ob wirklich 0 heraus kommt.
Hinweis 8
E(x) = -7x2 + 49x
Emax = E(3,5) = -7·3,52 + 49·3,5
Emax = -7·12,25 + 49·3,5
Emax = -85,75 + 171,5
Emax = 85,75
Der maximale Erlös von 85,75 GE wird bei einer Produktionsmenge von 3,5 ME erzielt.
Die Gewinnschelle xgs ist die Menge, bei der der Gewinn erstmals von negativen Gewinnen(Verlusten)
zu positiven Gewinnen übergeht.
Die Gewinnschwelle und die Gewinngrenze sind also Nullstellen der Gewinnfunktion.
Da die Gewinnschwelle xgs und die Gewinngrenze xgg Nullstellen der Gewinnfunktion sind,
muss die Gewinnfunktion G(x) zunächst gleich 0 gesetzt werden und dann nach x umgestellt werden.
Gewinnfunktion: G(x) = -x3 - x2 + 34x - 32
Da die Gleichung -x3 - x2 + 34x - 32 = 0
Bestimmung der Nullstellen der Funktion G(x) mit Geogebra:
c) Lösungshinweise zur Bestimmung der Gewinnschwelle (Break-even-Point) und der Gewinngrenze
Hinweis 1
Die Gewinngrenze xgg ist die Menge, bei der der Gewinn wieder von positiven Gewinnen
zu negativen Gewinnen (Verlusten) übergeht.
Hinweis 2
Hinweis 3
Hinweis 4
G(x) = 0
-x3 - x2 + 34x - 32 = 0
Hinweis 5
eine Funktion 3. Grades ist und ein Term ohne x (also -32) vorkommt, lässt sich diese Funktion manuell
, z.B. durch Ausklammern, nicht lösen. Es muss also ein Näherungsverfahren (z.B. Newton-Verfahren) oder Geogebra
zur Lösung herangezogen werden.
Hinweis 6
1. Möglichkeit:
In die Eingabezeile  von Geogebra eingeben: G(x)=-x^3-x^2+34x-32
von Geogebra eingeben: G(x)=-x^3-x^2+34x-32
Dann erscheint im Algebrabereich:
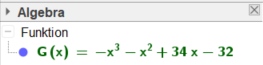
Dann in die Eingabezeile von Geogebra eingeben: Nullstelle(G(x), 0, 7)
Das bedeutet, dass Geogebra die Nullstelle zwischen x=0 und x=7 (Kapazitätsgrenze) berechnen soll.
Geogebra gibt im Algebrabereich aus:
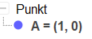 Geogebra berechnet also nur die Nullstelle x=1 im Intervall [0;7]. Es müsste aber noch eine weitere geben.
Geogebra berechnet also nur die Nullstelle x=1 im Intervall [0;7]. Es müsste aber noch eine weitere geben.
Der Graph der der Gewinnfunktion wird von Geogebra folgendermaßen angezeigt:
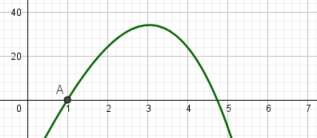
Geogebra hat also eben nur die erste Nullstelle im Intervall [0;7] berechnet. Um auch die zweite Nullstelle
zu berechnen, muss das Intervall so eingeschränkt werden, dass die zweite Nullstelle in dem Intervall liegt, die erste
Nullstelle aber nicht mehr, z.B.: Nullstelle(G(x), 4, 7)
Jetzt wird auch die 2. Nullstelle berechnet:

Die Lösung: Die Gewinnschwelle liegt bei einer Produktionsmenge von 1 ME. Die Gewinngrenze liegt bei einer
Produktionsmenge von 4,74 ME.
2. Möglichkeit:
Im CAS-Bereich von Geogebra eingeben:
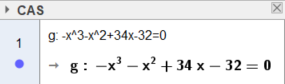
Wenn jetzt auf den Menüpunkt "Lösen"  geklickt wird,
wird die Gleichung exakt gelöst:
geklickt wird,
wird die Gleichung exakt gelöst:
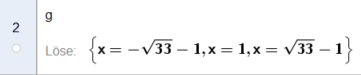
Wird stattdessen auf den Menüpunkt "Lösen numerisch"  geklickt, dann wird die Gleichung gerundet, also nur ungefähr, aber trotzdem sehr genau gelöst:
geklickt, dann wird die Gleichung gerundet, also nur ungefähr, aber trotzdem sehr genau gelöst:

Geogebra berechnet drei Lösungen der Gleichung -x3 - x2 + 34x - 32 = 0
x=-6,74 , x=1 und x=4,74
Dies sind also die Nullstellen der Funktion G(x), wobei x=-6,74 nicht im Dök einer Gewinnfunktion liegt,
da der Wert negativ ist. x=1 und x=4,74 liegen aber beide im ökonomisch sinnvollen
Definitionsbereich Dök = [0 ; 7] der Gewinnfunktion G(x).
Die Lösung: Die Gewinnschwelle liegt bei einer Produktionsmenge von 1 ME. Die Gewinngrenze liegt bei einer
Produktionsmenge von 4,74 ME.
Um den Stückpreis bei gewinnmaximaler Ausbringungsmenge unnd den maximalen Gewinn bestimmen zu können, muss
zunächst die gewinnmaximale Ausbringungsmenge berechnet werden. Dazu wird die Gewinnfunktion G(x) benötigt.
Um den Stückpreis bei gewinnmaximaler Ausbringungsmenge zu bestimmen, wir die Preisfunktion p(x) benötigt
Zunächst soll sich um Gmax und die zugehörige Menge gekümmert werden. Dazu muss zunächst die
Maximumstelle der Gewinnfunktion berechnet werden.
Da bei der Maximumstelle einer Funktion f die Steigung des Graphen der Funktion 0 ist und die Steigung einer
Funktion an jeder Stelle durch die Funktionwerte der 1. Ableitungsfunktion f' dieser Funktion bestimmt ist, muss
die 1. Ableitungsfunktion G' der Gewinnfunktion G bestimmt werden.
Bestimmung der 1. Ableitungsfunktion G' der Erlösfunktion G:
Bestimmung Maximumstelle von G also der Stelle, an der die Steigung der Funktion gleich 0 ist:
Der Gewinn ist maximal bei x = 3,05 ME. Jetzt soll zunächst der Stückpreis bei der gewinnmaximalen
Ausbringungsmenge berechnet werden.
x = 3,05 ME muss in die Preisfunktion eingesetzt werden, da diese ja zu jeder Menge x, die entsprechenden
Stückpreise als Funktionswerte hat.
d) Lösungshinweise zur Bestimmung des Stückpreises bei gewinnmaximaler Ausbringungsmenge und
des maximalen Gewinns
Hinweis 1
Hinweis 2
Hinweis 3
Hinweis 4
G(x) = -x3 - x2 + 34x - 32
G'(x) = -3x2 -2x + 34
Hinweis 5
G'(x) = 0
-3x2 -2x + 34 = 0
1. Möglichkeit: Lösen mit der pq-Formel
Da es sich um eine quadratische Gleichung handelt, kann diese mit der pq-Formel
(siehe auch das Thema "pq-Formel") gelöst werden.
Dazu muss die quadratische Gleichung zunächst in die Normalform x2 + px + q = 0 gebracht werden.
Beide Seiten der Gleichung müssen also durch -3 dividiert werden:
Es ergibt sich
und
Mit der pq-Formel ergibt sich dann:
x ≈ -3,72 liegt außerhalb des ökonomisch sinnvollen Definitionsbereichs
Dök = [0 ; 7]. Die einzig sinnvolle Extremstelle liegt also bei
x ≈ 3,05.
Jetzt muss formal noch gezeigt werden, dass x ≈ 3,05 eine Maximumstelle ist.
Dazu muss gelten G''(x) < 0.
G(x) = -x3 - x2 + 34x - 32
G'(x) = -3x2 -2x + 34
G''(x) = -6x - 2
G''(3,05) = -6 · 3,05 - 2 = -20,3 < 0
Der Gewinn ist also bei einer Menge von x = 3,05 ME maximal.
2. Möglichkeit: Lösen mit Geogebra
In Geogebra muss die Gleichung -3x2 -2x + 34 = 0 in den CAS-Bereich
eingegeben werden und dann auf "Lösen numerisch"
 geklickt werden:
geklickt werden:
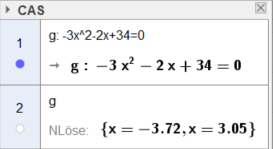
Und das Anzeigen der Gewinnfunktion mit Geogebra zeigt, dass bei x ≈ 3,05 das Maximum liegt.
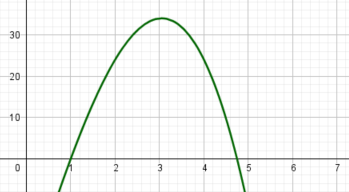
Der Gewinn ist also bei einer Menge von x = 3,05 ME maximal.
Hinweis 6
In welche Funktion muss jetzt x = 3,05 ME eingesetzt werden.
Hinweis 7
Hinweis 8
Stückpreis bei der gewinnmaximalen Ausbringungsmenge x = 3,05 ME:
p(x) = -7x + 49
p = p(3,05) = -7·3,05 + 49
p = -21,35 + 49
p = 27,65
Der Stückpreis bei der gewinnmaximalen Ausbringungsmenge x = 3,05 ME beträgt 27,65 GE/ME. Der Cournot'sche
Punkt ist also C(3,05 ME | 27,65 GE/ME).
Jetzt muss noch der maximale Gewinn Gmax berechnet werden. Der Gewinn ist maximal bei x = 3,05 ME.
Hinweis 9
In welche Funktion muss jetzt x = 3,05 ME eingesetzt werden.
x = 3,05 ME muss in die Gewinnfunktion eingesetzt werden, da diese ja zu jeder Menge x, die entsprechende Erlöse
als Funktionswerte hat.
Hinweis 10
Bemerkung: würde x = 3,05 in die erste Ableitungsfunktion G eingesetzt, dann würde 0 herauskommen.
Mit dem Ansatz G'(x)=0 wurde ja die gewinnmaximale Menge x = 3,05 durch Umstellen berechnet. Würde man also
x = 3,05 wieder in G'(x) einsetzen, wird nur die Probe gemacht, ob wirklich 0 heraus kommt.
Berechnung des maximalen Gewinns Gmax:
Hinweis 11
G(x) = -x3 - x2 + 34x - 32
Gmax = G(3,05) = -3,053 - 3,052 + 34·3,05 - 32
Gmax ≈ -28,37 - 9,30 + 103,7 - 32
Gmax = 34,03
Der maximale Gewinn von 34,03 GE wird bei einer Produktionsmenge von 3,05 ME erzielt.
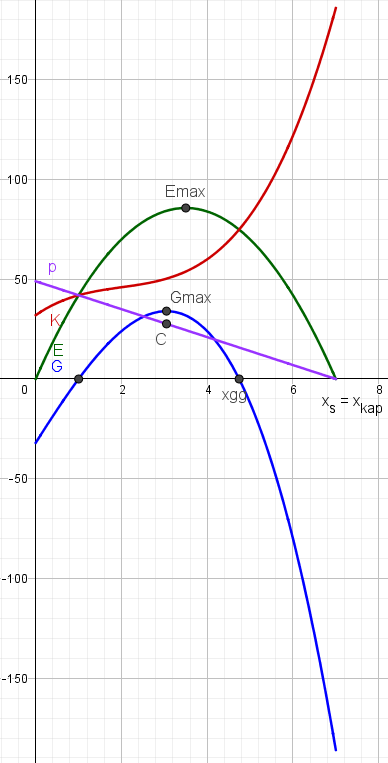
e) Zeichnung aller Funktion und der bestimmten Werte bzw. Stellen mit Geogebra
Wenn Du auf die Schaltfläche "Weiter" klickst, dann kommst Du zurück zu der Startseite von WuLf.



