Thema: Kostenfunktion, Erlösfunktion, Gewinnfunktion und deren Zusammenhang im Polypol und Monopol

In diesem Abschnitt werden die Zusammenhänge von Gewinn, Kosten und Erlösen für eine bestimmte Produktionsmenge auf eine beliebige Produktionsmenge des gleichen Produktes erweitert. Gewinn, Kosten und Erlös werden dann als mathematische Funktionen dargestellt, die abhängig von der Produktionsmenge x sind.

Gesamtkostenfunktion K(x)

Die Gesamtkosten setzen sich aus den variablen Kosten K_v, die von der Produktionsmenge x abhängen und den Fixkosten K_f zusammen, die nicht von der Produktionsmenge x abhängen:

K(x) = K_v(x) + K_f

Einige Überlegungen führen zu den folgenden Schlussfolgerungen:

Es können minimal x = 0 Produkte produziert und maximal soviele, wie sich mit den Mitarbeitern, Maschinen, der vorhandenen Zeit usw. herstellen lassen. Diese maximale Produktionmenge wird Kapazitätsgrenze x_kap genannt.
--> Daraus lässt sich schließen, dass der ökonomisch sinnvolle Definitionsbereich D_ök einer Gesamtkostenfunktion 0 <= x <= x_kap oder in Intervallschreibweise ausgedrückt D_ök = [ 0 ; x_kap ] ist.

Es ist klar, dass die Produktionskosten steigen, wenn die Produktionsmenge steigt, also wenn mehr von dem gleichen Produkt produziert wird.
--> Daraus lässt sich schließen, dass eine Gesamtkostenfunktion immer eine positive Steigung haben muss, d.h. K'(x) > 0 in D_ök. Man sagt auch, dass die Gesamtkostenfunktion streng monoton steigen muss.

Bei einer Produktionsmenge von x = 0, d.h. wenn nichts produziert wird, entstehen keine variablen Kosten: K_v(0) = 0
--> Es bleiben bei einer Produktionsmenge von x = 0 nur die Fixkosten K_f als Gesamtkosten übrig.
K(0) = K_v(0) + K_f = 0 + K_f = K_f
--> Daraus lässt sich schließen, dass der Graph der Gesamtkostenfunktion die Kostenachse immer bei den Fixkosten K_f, schneidet, wobei die Fixkosten immer größer als 0 sind.
--> Daraus lässt sich wiederum schließen, dass der ökonomisch sinnvolle Wertebereich W_ök einer Gesamtkostenfunktion K(x) >= 0 oder in Intervallschreibweise ausgedrückt W_ök = [ 0 ; K(x_kap) ] ist.

Da eine Gesamtkostenfunktion hervorgehend aus den vorherigen Überlegungen einen D_ök = [ 0 ; x_kap ] und einen W_ök = [ 0 ; K(x_kap) ] hat, ...
--> ... lässt sich daraus schließen, dass der Graph der Gesamtkostenfunktion K(x) ausschließlich im 1. Quadranten des Koordinatensystems verläuft, in dem es nur positive Koordinaten gibt.

Die ertragsgesetzliche Gesamtkostenfunktion K(x)

Die Bedingungen für eine Gesamtkostenfunktion wurden eben hergeleitet. Damit sind aber viele mögliche Verläufe für eine Gesamtkostenfunktion, z.B. ein linearer Verlauf (visuell eine Gerade) oder ein parabelförmiger Verlauf denkbar, hauptsache die oben genannten Bedingungen sind erfüllt.

Einen sehr realitätsnahen Verlauf hat die sogenannte ertragsgesetzliche Gesamtkostenfunktion. Sie wird auch fälschlicherweise teilweise s-förmige Gesamtkostenfunktion genannt. Wenn überhaupt sollte man sie ?-förmige Gesamtkostenfunktion, wegen ihres in etwa fragezeichenförmigen Verlaufs, nennen. Besser ist aber der Name ertragsgesetzliche Gesamtkostenfunktion.
Die ertragsgesetzliche Gesamtkostenfunktion lässt sich am einfachsten durch eine ganzrationale Funktion 3. Grades beschreiben.

K(x) = ax³ + bx² + cx + d mit

K_v(x) = ax³ + bx² + cx und K_f = d

In der folgenden Abbildung ist der Graph der Gesamtkostenfunktionen K(x) = x³ - 6x² + 15x + 32 visualisiert.

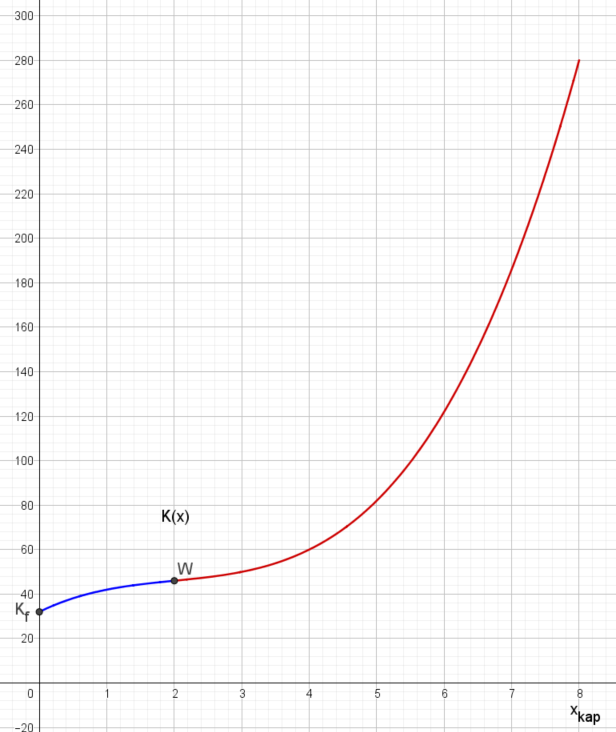
Die dargestellte Gesamtkostenfunktion hat alle Eigenschaften, die eine Gesamtkostenfunktion haben muss:

D_ök = [0 ; x_kap] = [0 ; 8]. Es können also mit den vorhandenen Mitteln zwischen 0 und 8 Mengeneinheiten (ME) produziert werden.

K(x) steigt streng monoton. Von x = 0 ME fallen bei steigenden Produktionmengen auch immer höhere Kosten an.

Die Fixkosten betragen K_f = K(0) = 0³ - 6·0² + 15·0 + 32 = 32 ME .
W_ök = [K_f ; K(x_kap)] = [32 ; K(8)] = [32 ; 8³ - 6·8² + 15·8 + 32] = [32 ; 280]
Es entstehen also Kosten zwischen 32 und 280 Geldeinheiten (GE).

K(x) verläuft ausschließlich im 1. Quadranten, in dem alle Koordinaten ausschließlich positiv sind.

Darüber hinaus hat die ertragsgesetzliche Gesamtkostenfunktion im blauen Bereich eine Rechtskrümmung, die im Wendepunkt W bei einer Produktionsmenge von x = 2 ME in eine Linkskrümmung übergeht. D.h. die positive Steigung von K(x) nimmt bis W immer mehr ab. Im Wendepunkt W hat sie ihre geringste Steigung. Danach (im roten Bereich) nimmt die positive Steigung dann immer mehr zu. Man sagt auch: Die ertragsgesetzliche Kostenfunktion steigt zunächst degressiv (blauer Bereich mit Rechtskrümmung) und dann progessiv (roter Bereich mit Linksskrümmung).

Dieser Verlauf ist sehr realitätsnah: Wegen des effizienteren Arbeitskräfte-/Maschineneinsatzes (z.B. noch keine Überstundenzuschläge und moderatem Maschinenverschleiß) steigen die Gesamtkosten zunächst degressiv (Rechtskrümmung). Bei einer Ausweitung der Produktion fallen dann z.B. immer mehr Überstundenzuschläge an und die Maschinen haben einen überdurchschnittlichen Verschleiß. Dies ist hier ab einer Produktionsmenge von 2 ME (Wendestelle) der Fall. Die Gesamtkosten steigen nun progressiv an (Linkskrümmung).

Erlösfunktion E(x)

Jedes Produkt, das hergestellt wird, hat einen Stückpreis. Wenn es sich um eine Dienstleistung handelt, dann hat diese einen Preis pro Stück Zeit, meist pro Stunde.
Um den Erlös zu berechnen, muss der Stückpreis p mit der Menge x des verkauften Produktes multipliziert werden.
Zunächst einmal kann also festgehalten werden, dass E(x) = p·x ist.

Polypol (Vollständige Konkurrenz)

Herrscht auf einem Markt vollständige Konkurrenz, dann wird von einem Polypol gesprochen. Das Polypol ist eine Art von Markt, auf dem es viele Anbieter und viele Nachfrager gibt. Es ist also ein Markt mit vielen verschiedenen Unternehmen, die ähnliche Produkte oder Dienstleistungen anbieten und vielen Kunden, die diese Produkte kaufen möchten.
In einem Polypol gibt es keinen einzelnen Anbieter oder Käufer, der den Markt dominieren kann. Jeder Anbieter hat nur einen kleinen Anteil am Gesamtmarkt und jeder Käufer hat nur einen kleinen Anteil an der Gesamtnachfrage.
Da es viele Anbieter gibt, herrscht in einem Polypol normalerweise ein hoher Wettbewerb. Die Unternehmen müssen sich bemühen, ihre Produkte oder Dienstleistungen attraktiver oder günstiger anzubieten als ihre Konkurrenten, um Kunden anzulocken. Dies führt oft zu niedrigeren Preisen und einer größeren Auswahl für die Verbraucher.
Im Polypol gibt es auch keine Markteintrittsbarrieren, das heißt, neue Unternehmen können relativ leicht in den Markt eintreten und mit den bestehenden Unternehmen konkurrieren. Dies trägt ebenfalls zur Wettbewerbsintensität bei.
Das Polypol ist also ein Markt, auf dem viele Anbieter und viele Nachfrager existieren, es herrscht Wettbewerb und die Unternehmen haben nur einen begrenzten Einfluss auf den Markt.
Dies hat Auswirkungen auf die Preisbildung. In einem Polypol haben die Anbieter/Nachfrager keinen Einfluss auf den Preis und ändern lediglich die Menge eines Produkts, die sie herstellen/anbieten oder kaufen (Mengenanpasser). Das bedeutet, die Unternehmen verfügen nur über eine geringe Marktmacht. Im Falle einer Preiserhöhung könnten die Nachfrager sofort zu einem neuen Anbieter wechseln. Ebenso haben die Nachfrager wenig Verhandlungsspielraum. Wenn sie den Preis für ein Produkt senken wollen, beschließt der Anbieter, es nicht zu verkaufen, weil es noch viele andere Kunden gibt. Das bedeutet wiederum, dass der Stückpreis sich auf einen konstanten Wert einpendelt, egal wieviel Stück davon verkauft/gekauft werden.

Die Preisfunktion (auch Preis-Absatz-Funktion) des polypolistischen Anbieters lautet also:

p(x) = p mit p > 0

Der Preis p ist eine Konstante, also unabhängig von der Menge x, z.B. p = 20 GE (Geldeinheiten).

Für das Beispiel wäre p(x) = 20.

Daraus ergibt sich die Erlösfunktion E(x) für das Polypol:

E(x) = p(x)·x = p·x

Im folgenden Beispiel ist p = 20 GE, d.h. es ergibt sich die Funktion E(x) = 20·x = 20x , wobei die Kapazitätsgrenze wieder bei x_kap = 8 ME liegen soll:

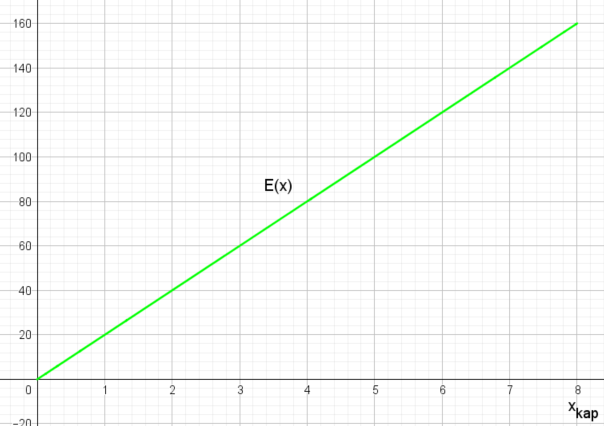
Die dargestellte Erlösfunktion im Polypol hat alle Eigenschaften, die eine Erlösfunktion haben muss:

D_ök = [0 ; x_kap] = [0 ; 8]. Es können also zwischen 0 und 8 Mengeneinheiten (ME) auf dem Markt angeboten werden.

E(x) steigt streng monoton. Von x = 0 ME steigen bei steigenden Absatzmengen auch die Erlöse immer mehr an.

Bei einem Absatz von 0 ME wird auch kein Erlös erzielt.
W_ök = [0; E(x_kap)] = [0 ; E(8)] = [0 ; 20·8] = [0 ; 160]
Es entstehen also Erlöse zwischen 0 und 160 Geldeinheiten (GE).

E(x) verläuft ausschließlich im 1. Quadranten, in dem alle Koordinaten ausschließlich positiv sind.

Monopol (Angebotsmonopol)

Ein Monopol ist eine Marktform, bei der es nur einen einzigen Anbieter oder Verkäufer gibt, der ein bestimmtes Produkt oder eine bestimmte Dienstleistung kontrolliert. Das bedeutet, dass es keine anderen Unternehmen gibt, die das gleiche Produkt oder die gleiche Dienstleistung anbieten können.
Das Unternehmen, das das Monopol besitzt, hat die volle Kontrolle über den Markt. Es kann den Preis für sein Produkt oder seine Dienstleistung festlegen, da es keine Konkurrenz gibt, die den Preis beeinflussen könnte. Das Unternehmen kann daher oft höhere Preise verlangen, da die Kunden keine andere Wahl haben.
Ein Monopol kann entstehen, wenn ein Unternehmen eine bestimmte Technologie, ein Patent oder eine andere Art von Vorteil besitzt, der es anderen Unternehmen schwer macht, in den Markt einzutreten und zu konkurrieren. Es kann auch entstehen, wenn ein Unternehmen durch Fusionen oder Übernahmen andere Unternehmen aufkauft und so den Markt beherrscht.

Einige Überlegungen führen zu den folgenden Schlussfolgerungen für eine Preis-Absatzfunktion im Monopol:

Es ist klar, dass bei höherem Stückpreis weniger Produkte nachgefragt werden und bei niedrigerem Stückpreis mehr Produkte nachgefragt werden.
--> Daraus lässt sich schließen, dass eine Preisfunktion im Monopol immer eine negative Steigung haben muss, d.h. p'(x) < 0 in D_ök. Man sagt auch, dass die Preisfunktion streng monoton fallen muss.

Es können minimal x = 0 Produkte angeboten werden. Maximal kann ein Betrieb nur x = x_kap ME produzieren. Bei der Preis-Absatzfunktion im Monopol ist aber auch noch eine andere Größe wichtig, nämlich die sogenannte Sättigungsgrenze x_s. Die Sättigungsgrenze im Monopol bezieht sich auf die maximale Menge an Produkten oder Dienstleistungen, die ein monopolistisches Unternehmen verkaufen kann, bevor die Nachfrage abnimmt und der Markt gesättigt ist.
Wenn ein Unternehmen ein Monopol hat, bedeutet das, dass es der einzige Anbieter auf dem Markt ist und keine Konkurrenz hat. Anfangs kann das Unternehmen möglicherweise große Mengen seines Produkts verkaufen, da es keine Alternativen gibt und die Nachfrage hoch ist.
Jedoch gibt es eine Grenze, wie viel von einem Produkt die Kunden kaufen möchten. Wenn das Unternehmen diese Sättigungsgrenze erreicht, bedeutet dies, dass die Nachfrage nach dem Produkt abnimmt, da die meisten Kunden bereits das Produkt gekauft haben oder nicht mehr daran interessiert sind.
--> Daraus lässt sich schließen, dass der ökonomisch sinnvolle Definitionsbereich D_ök einer Preisfunktion im Monopol 0 <= x <= x_s oder in Intervallschreibweise ausgedrückt D_ök = [ 0 ; x_s ] ist.

Bei einer Produktionsmenge von nahezu x = 0, d.h. wenn nahezu nichts produziert wird, ist der Stückpreis am höchsten
p(0) = p_max
--> Daraus lässt sich schließen, dass der Graph der Preisfunktion im Monopol die Preisachse immer bei dem Höchstpreis p_max schneidet, wobei der Höchstpreis immer größer als 0 ist.
Bei einer Produktionsmenge an der Sättigungsgrenze x_s liegt der niedrigste Stückpreis p_min.
--> Daraus lässt sich wiederum schließen, dass der ökonomisch sinnvolle Wertebereich W_ök einer Preisfunktion im Monopol p_min <= p(x) <= p_max oder in Intervallschreibweise ausgedrückt W_ök = [ p_min ; p_max ] ist.

Da eine Preisfunktion im Monopol hervorgehend aus den vorherigen Überlegungen einen D_ök = [ 0 ; x_s ] und einen W_ök = [ p_min ; p_max ] hat, ...
--> ... lässt sich daraus schließen, dass der Graph der Preisfunktion p(x) im Monopol ausschließlich im 1. Quadranten des Koordinatensystems verläuft, in dem es nur positive Koordinaten gibt.

Im folgenden Beispiel ist die einfachste Form einer Preisfunktion im Monopol gezeichnet. Sie hat einen linearen Verlauf und einen minimalen Preis von 0 GE. Darüber hinaus soll sie eine Sättigungsgrenze von x_s = 7 ME haben und einen maximalen Preis von p_max = 84 GE haben, d.h. es ergibt sich die Funktion p(x) = -12x + 84 .

Und damit ergibt sich die Erlösfunktion:

E(x) = p(x)·x = (-12x + 84)·x = -12x² + 84x :

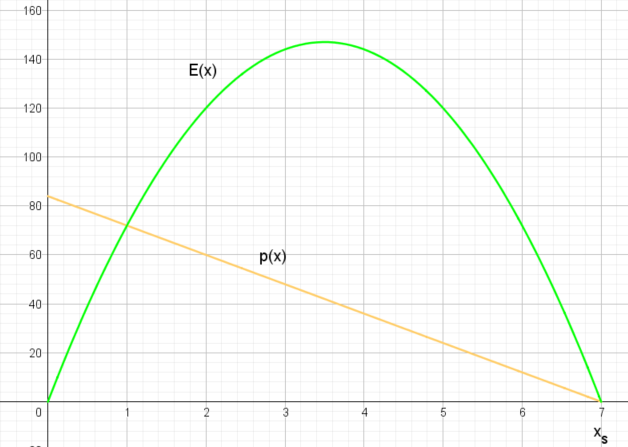
Erloesfunktion_im_Monopol

Die dargestellte Preisfunktion (gelb) hat alle Eigenschaften, die eine Preisfunktion im Monopol haben muss:

D_ök = [0 ; x_s] = [0 ; 7]. Es sollten also zwischen 0 und 7 Mengeneinheiten (ME) auf dem Markt angeboten werden.

p(x) fällt streng monoton. Von x = 0 ME sinkt bei steigenden Absatzmengen auch der Preis immer mehr.

Bei einem Absatz von 0 ME wird der höchste Preis p_max = 84 GE erzielt.
Bei einem Absatz von 7 ME bei der Sättigungsgrenze wird der niedrigste Preis mit 0 GE erzielt.
W_ök = [p_min; p_max] = [0 ; 84].

p(x) verläuft ausschließlich im 1. Quadranten, in dem alle Koordinaten ausschließlich positiv sind.

Bei einer solchen linearen streng monton fallenden Preisfunktion im Monopol (gelb) mit einem minimalen Preis von p_min = 0 GE ergibt sich immer eine Erlösfunktion E(x), deren Graph eine nach unten geöffnete Parabel ist (grün), die ausschließlich im 1. Quadranten verläuft, ihre Nullstellen bei x = 0 und x = x_s und ihr Maximum bei

\frac{x_{s}}{2}

hat.

Gewinnfunktion G(x)

Die Gewinnfunktion ergibt sich als Differenz aus Erlösfunktion E(x) und Gesamtkostenfunktion K(x), unabhängig davon, ob der Markt ein Polypol oder ein Monopol ist:

G(x) = E(x) - K(x) bzw. G(x) = p(x)·x - K(x)

Sie gibt für jede Produktionsmenge x im Definitionsbereich

D_ök = [0 ; x_s], falls x_s < x_kap

bzw.

D_ök = [0 ; x_s], falls x_kap < x_s

den Gewinn an.

Beispiel: Gewinn im Polypol

Für die Erlösfunktion E(x) = 20x (grün) und die ertragsgesetzliche Gesamtkostenfunktion K(x) = x³ - 6x² + 15x + 32 (rot) sowie die Kapazitätsgrenze x_kap = 8 ME und die Sättigungsgrenze x_s = 10 ME ergibt sich die Gewinnfunktion (blau):

G(x) = E(x) - K(x)

G(x) = 20x - (x³ - 6x² + 15x + 32)

G(x) = 20x - x³ + 6x² - 15x - 32)

G(x) = -x³ + 6x² - 15x + 20x - 32

G(x) = -x³ + 6x² + 5x - 32
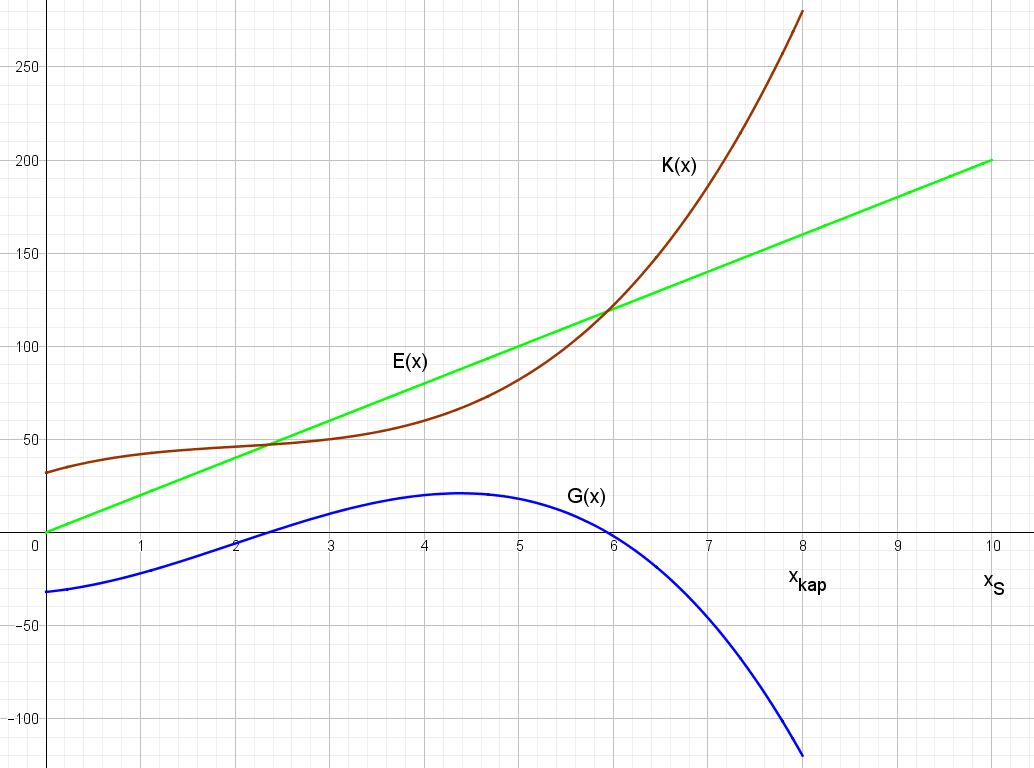
Kosten_Erlöse_Gewinne_im_Polypol

Es kann anhand der Graphen folgendes festgestellt werden:

Für die Mengen x, für die K(x) oberhalb von E(x) verläuft, die Kosten also größer als die Erlöse sind, verläuft G(x) unterhalb der x-Achse. Hier sind die Gewinne also negativ. Man spricht auch von Verlusten.

Für die Mengen x, für die K(x) unterhalb von E(x) verläuft, die Kosten also geringer als die Erlöse sind, verläuft G(x) oberhalb der x-Achse. Hier sind die Gewinne also positiv. Es wird also "echter" Gewinn gemacht.

Die Nullstellen von G(x) sind gleichzeitig die Schnittstellen von E(x) und K(x). Bei den Schnittstellen von E(x) und K(x) sind die Erlöse und Kosten genau gleich. D.h., dass dort die Gewinne genau 0 GE betragen.

Die erste Nullstelle von G(x) wird Gewinnschwelle genannt (x≈2,4), da dort bei steigenden Mengen x der Übergang von Verlusten zu "echten" Gewinnen liegt.
Die zweite Nullstelle von G(x) wird Gewinngrenze genannt (x≈5,9), da dort bei steigenden Mengen x der Übergang von "echten" Gewinnen zu Verlusten liegt. Ab der Gewinngrenze werden bei steigenden Mengen x nur noch Verluste "eingefahren".

Der größte Gewinn wird an der Maximumstelle von G(x) gemacht (x≈4,4). An dieser Stelle liegt E(x) mit größtem Abstand über K(x).

Beispiel: Gewinn im Monopol

Für die Erlösfunktion E(x) = -12x² + 84x (grün) und die ertragsgesetzliche Gesamtkostenfunktion K(x) = x³ - 6x² + 15x + 32 (rot) sowie die Kapazitätsgrenze x_kap = 8 ME und die Sättigungsgrenze x_s = 7 ME ergibt sich die Gewinnfunktion (blau):

G(x) = E(x) - K(x)

G(x) = -12x² + 84x - (x³ - 6x² + 15x + 32)

G(x) = -12x² + 84x - x³ + 6x² - 15x - 32)

G(x) = -x³ + 6x² -12x² - 15x + 84x - 32

G(x) = -x³ - 6x² + 69x - 32

Kosten_Erlöse_Gewinne_im_Monopol

In der Abbildung mit den Graphen lassen sich eine Gewinnschwelle bei x≈0,5 ME, eine Gewinngrenze bei x≈5,5 ME und die Maximumstelle des Gewinns bei x≈3,2 ME ablesen.

Spielwiese (Internetverbindung erforderlich)

Mit der folgenden GeoGebra-Anwendung lassen sich über die Schieberegler verschiedene Preisfunktionen p(x) (gelb) mit pmin (minimaler Preis bei der Sättigungsgrenze xs), pmax (Höchstpreis) und xs (Sättigungsgrenze) und ertragsgesetzliche Kostenfunktionen K(x)=ax³ + bx² +cx + Kf (rot) einstellen. Diese werden dann angezeigt. Zusätzlich werden die sich dann ergebenden Erlösfunktionen E(x) (grün) und Gewinnfunktionen G(x) (blau) angezeigt.

Wenn Du auf die Schaltfläche "Weiter" klickst, dann kommt eine Aufgabe zu Kosten, Erlösen und Gewinnen.

Klicke auf "Weiter".

Webprogrammierung und Inhalt: Dr. Dag Pechtel