Thema: Aufgabe zum Differenzieren (Ableiten) von ganzrationalen Funktionen
Aufgabe:
Gegeben sei die ganzrationale Funktion f(x) = 0,001x5 − 0,002x4 − 0,05x3 + 0,1x2 + 0,625x − 1.25
Die Funktion hat keine Sattelpunkte.
- Bestimme die Ableitungsfunktion f '(x).
- Zeichne den Graphen der Ableitungsfunktion f '(x).
- Bestimme nur mit Hilfe des Graphen der Ableitungsfunktion durch Ablesen und durch Einsetzen von Werten in die Funktionsgleichung von f(x), die Extrempunkte und die Wendepunkte von f(x). Der Graph der Funkjtion f(x) soll nicht gezeichnet werden.
Probiere es erst ohne jeglichen Hinweis. Herauskommen müsste die folgende Ableitungsfunktion
f '(x) = 0,005x4 - 0,008x3 - 0,15x2 + 0,2x + 0,625
der folgende Graph der Ableitungsfunktion:
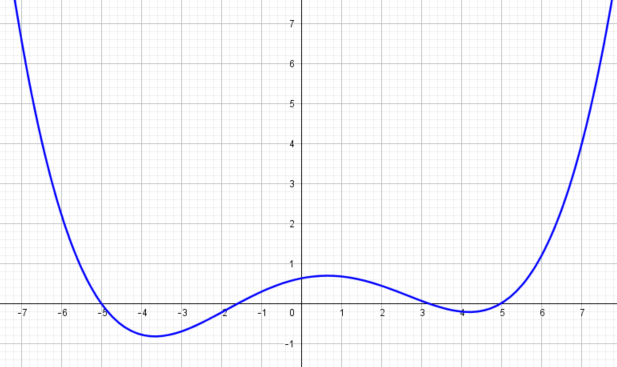
und die folgenden Hoch-, Tief- und Wendepunkte der Originalfunktion f(x):
H1 = (-0,5|0), W1 = (-3,6|-0,81), T1 = (-1,6|-1,73), W2 = (0,6|-0,85), H2 = (3,2|0,26), W3 = (4,2|0,16), T2 = (5|0),
Eine ganzrationale Funktion ist aus mehreren Potenzfunktionen und meist auch einer konstanten Funktion zusammengesetzt. Diese einzelnen
Potenzfunktionen bzw. die konstante Funktion können jeweils einzeln mit der Potenz- und der Vorfaktorregel bzw. der Konstantenregel
abgeleitet werden.
Hinweis 1
Die Funktion besteht aus 5 Potenzfunktionen und einer konstanten Funktion.
Hinweis 2
Es handelt sich um die 5 Potenzfunktionen:
Hinweis 3
f1(x) = 0,001x5
f2(x) = −0,002x4
f3(x) = −0,05x3
f4(x) = +0,1x2
f5(x) = +0,625x
und die konstante Funktion
f6(x) = − 1.25
Die 6 Teilfunktionen haben die folgenden Ableitungen:
Hinweis 4
f1(x) = 0,001x5 ⇒ f1'(x) = 5⋅0,001x5-1 = 0,005x4
f2(x) = −0,002x4 ⇒ f2'(x) = 4⋅(-0,002x)4-1 = -0,008x3
f3(x) = −0,05x3 ⇒ f3'(x) = 3⋅(-0,05x)3-1 = -0,15x2
f4(x) = +0,1x2 ⇒ f4'(x) = 2⋅0,1x2-1 = 0,2x1 = 0,2x
f5(x) = +0,625x = +0,625x1 ⇒ f5'(x) = 1⋅0,625x1-1 = 0,625x0 = 0,625⋅1 = 0,625
und die konstante Funktion
f6(x) = − 1.25 ⇒ f6'(x) = 0
Die komplette Ableitungsfunktion f '(x) ergibt sich, in dem die Teilableitungsfunktionen f1'(x) - f6'(x) addiert werden.
Hinweis 5
f '(x) = f1'(x) + f2'(x) + f3'(x) + f4'(x) +f5'(x) + f6'(x)
Hinweis 6
f '(x) = (0,005x4) + (-0,008x3) + (-0,15x2) + (0,2x) + (0,625) + (0)
Hinweis 7
f '(x) = 0,005x4 - 0,008x3 - 0,15x2 + 0,2x + 0,625 + 0
f '(x) = 0,005x4 - 0,008x3 - 0,15x2 + 0,2x + 0,625
Die Ableitungsfunktion f '(x) lautet: f '(x) = 0,005x4 - 0,008x3 - 0,15x2 + 0,2x + 0,625
Zeichne die Funktion entweder mit Geogebra oder erstelle eine Wertetabelle von x = -7 bis x = +7 zeichen die Punkte in ein
Koordinatensystem ein und verbinde die Pukte sinnvoll.
Hinweis 8
Wertetabelle:
Hinweis 9
x -7 -6 -5 -4 -3 -2 -1
0 1 2 3 4 5 6 7
f '(x) 6,62 2,23 0 -0,78 -0,7 -0,23 0,29
0,63 0,67 0,44 0,06 -0,21 0 1,18 3,94
Geogebra:

Der Graph von f '(x) hat Nullstellen. Was bedeutet das für die Originalfunktion f(x)?
Hinweis 10
Bei den Nullstellen der Ableitungsfunktion f '(x) hat die Originalfunktion f(x) die Steigung 0. An welchen Stellen hat die
Originalfunktion f(x) die Steigung 0?
Hinweis 11
Die Originalfunktion f(x) hat an Extrempunkten und Sattelpunkten die Steigung 0. Hier in dieser Aufgabenstellung hat die Originalfunktion
f(x) keine Sattelpunkte (siehe oben). Also handelt es sich bei den Nullstellen der Ableitungsfunktion f '(x) um Minimum- bzw. Maximumstellen.
Hinweis 12
Die Nullstellen der Ableitungsfunktion liegen abgelesen ungefähr bei x = -5 ; x = -1,6 ; x = 3,2 ; x = 5. Dies sind
also die Extremstellen der Originalfunktion f(x).
Hinweis 13
Wie findest Du anhand des Graphen der Ableitungsfunktion f '(x) heraus, ob die Extremstellen x = -5 ; x = -1,6 ; x = 3,2 ; x = 5
Minimum- oder Maximumstellen sind?
Hinweis 14
Um anhand des Graphen der Ableitungsfunktion f '(x) herauszufinden, ob die Extremstellen x = -5 ; x = -1,6 ; x = 3,2 ; x = 5
Minimum- oder Maximumstellen sind, musst Du Dir die Funktionswerte links und rechts neben diesen Stellen der Ableitungsfunktion f '(x)
anschauen. Dabei ist nur wichtig, ob die Funktionswerte der Ableitungsfunktion f '(x) dort positiv oder negativ sind, denn dann ist die Steigung
der Originalfunktion dort positv oder negativ.
Hinweis 15
Fange mit der ersten Nullstelle x = -5 der Ableitungsfunktion f '(x) an. Kurz vor x = -5 hat f '(x) positive Funktionswerte.
Kurz nach x = -5 hat f '(x) negative Funktionswerte. D.h. vor der Extremstelle x = -5 der Originalfunktion f(x) ist die Steigung positiv
und nach der Extremstelle x = -5 ist die Steigung negativ. Ist das bei Hoch- oder Tiefpunkten der Fall?
Hinweis 16
Wenn vor der Extremstelle x = -5 die Steigung der Originalfunktion f(x) positiv
und nach der Extremstelle x = -5 negativ ist, dann muss es sich um einen Hochpunkt handeln, da der Graph einer Funktion bis zum Hochpunkt steigt
und danch wieder fällt. Bei einem Tiefpunkt wäre das genau anders herum.Hinweis 17
Bei x = -5 hat der Graph von f(x) also einen Hochpunkt. Wie wird jetzt die y-Koordinate dieses Hochpunktes bestimmt?
Um die y-Koordinate des Hochpunktes zu bestimmen, muss die Maximumstelle x = -5 in die Funktionsgleichung der Originalfunktion f(x)
eingesetzt werden.
Hinweis 18
Bestimmung der y-Koordinate des Hochpunktes durch Einsetzen der Maximumstelle x = -5 in die Funktionsgleichung
f(x) = 0,001x5 − 0,002x4 − 0,05x3 + 0,1x2 + 0,625x − 1.25
Hinweis 19
f(-5) = 0,001⋅(-5)5 − 0,002⋅(-5)4 − 0,05⋅(-5)3
+ 0,1⋅(-5)2 + 0,625⋅(-5) − 1.25
f(-5) = 0,001⋅(-3125) − 0,002⋅(+625) − 0,05⋅(-125)
+ 0,1⋅(+25) + 0,625⋅(-5) − 1.25
f(-5) = -3,125 − 1.25 + 6,25 + 2,5 -3,125 − 1.25
f(-5) = 0
Wie lautet jetzt der erste Hochpunkt der Funktion f(x) ?
Der erste Hochpunkt der Funktion f(x) lautet H1 = (-0,5 | 0)
Hinweis 20
Für die anderen Hoch- und Tiefpunkte wird jetzt nach dem gleichen Prinzip vorgegangen.
Die Berechnungen für die weiteren Hoch und Tiefpunkte gehen folgendermaßen:
Hinweis 21
Extremstelle x = -1,6: Links von x = -1,6 sind die Funktionswerte von f '(x) negativ und rechts positiv.
Das bedeutet, dass f(x) an dieser Stelle von einer negativen Steigung in eine positive übergeht. Das ist nur bei Tiefpunkten
der Fall.
Bestimmen der y-Koordinate des Tiefpunktes:
f(-1,6) = 0,001⋅(-1,6)5 − 0,002⋅(-1,6)4 − 0,05⋅(-1,6)3
+ 0,1⋅(-1,6)2 + 0,625⋅(-1,6) − 1.25 = -1,73
Daraus folgt der Tiefpunkt T1 = (-1,6 | -1,73)
Extremstelle x = 3,2: Links von x = 3,2 sind die Funktionswerte von f '(x) positiv und rechts negativ.
Das bedeutet, dass f(x) an dieser Stelle von einer positiven Steigung in eine negative übergeht. Das ist nur bei Hochpunkten
der Fall.
Bestimmen der y-Koordinate des Hochpunktes:
f(3,2) = 0,001⋅(3,2)5 − 0,002⋅(3,2)4 − 0,05⋅(3,2)3
+ 0,1⋅(3,2)2 + 0,625⋅(3,2) − 1.25 = 0,26
Daraus folgt der Hochpunkt H2 = (3,2 | 0,26)
Extremstelle x = 5: Links von x = 5 sind die Funktionswerte von f '(x) negativ und rechts positiv.
Das bedeutet, dass f(x) an dieser Stelle von einer negativen Steigung in eine positive übergeht. Das ist nur bei Tiefpunkten
der Fall.
Bestimmen der y-Koordinate des Tiefpunktes:
f(5) = 0,001⋅(5)5 − 0,002⋅(5)4 − 0,05⋅(5)3
+ 0,1⋅(5)2 + 0,625⋅(5) − 1.25 = 0
Daraus folgt der Tiefpunkt T2 = (5 | 0)
Der Graph von f '(x) hat neben den Nullstellen auch noch drei Extremstellen. Was bedeutet das für die Originalfunktion f(x)?
Hinweis 22
Bei den Extremstellen der Ableitungsfunktion f '(x) hat die Originalfunktion f(x) die größten negativen bzw. positiven Steigungen.
An welchen Stellen hat die Originalfunktion f(x) die größten negativen bzw. positiven Steigungen?
Hinweis 23
Die Originalfunktion f(x) hat an Wendepunkten die größten negativen bzw. positiven Steigungen.
Hinweis 24
Die Extremstellen der Ableitungsfunktion liegen abgelesen ungefähr bei x = -3,6 ; x = 0,6 ; x = 4,2. Dies sind
also die Wendestellen der Originalfunktion f(x).
Hinweis 25
Fangen wir mit der ersten Extremstelle der Ableitungsfunktion x = -3,6 an.
Um die y-Koordinate des Hochpunktes zu bestimmen, muss die Extremstelle x = -3,6 in die Funktionsgleichung der Originalfunktion f(x)
eingesetzt werden.
Hinweis 26
Bestimmung der y-Koordinate des Wendepunktes durch Einsetzen der Wendestelle x = -3,6 in die Funktionsgleichung
f(x) = 0,001x5 − 0,002x4 − 0,05x3 + 0,1x2 + 0,625x − 1.25
Hinweis 27
f(-3,6) = 0,001⋅(-3,6)5 − 0,002⋅(-3,6)4 − 0,05⋅(-3,6)3
+ 0,1⋅(-3,6)2 + 0,625⋅(-3,6) − 1.25
f(-3,6) = -0,81
Wie lautet jetzt der erste Wendepunkt der Funktion f(x) ?
Der erste Wendepunkt der Funktion f(x) lautet W1 = (-3,6 | -0,81)
Hinweis 28
Für die anderen Wendepunkte wird jetzt nach dem gleichen Prinzip vorgegangen.
Die Berechnungen für die weiteren Wendepunkte gehen folgendermaßen:
Hinweis 29
Wendestelle x = 0,6:
Bestimmen der y-Koordinate des Wendepunktes:
f(0,6) = 0,001⋅(0,6)5 − 0,002⋅(0,6)4 − 0,05⋅(0,6)3
+ 0,1⋅(0,6)2 + 0,625⋅(0,6) − 1.25 = -0,85
Daraus folgt der Wendepunkt W2 = (0,6 | -0,85)
Wendestelle x = 4,2:
Bestimmen der y-Koordinate des Wendepunktes:
f(4,2) = 0,001⋅(4,2)5 − 0,002⋅(4,2)4 − 0,05⋅(4,2)3
+ 0,1⋅(4,2)2 + 0,625⋅(4,2) − 1.25 = 0,26
Daraus folgt der Wendepunkt W3 = (4,2 | 0,16)
Wenn Du auf die Schaltfläche "Weiter" klickst,
dann geht es irgendwann im Laufe dieses Schuljahres mit der Ableitung verketteter Funktionen weiter.



