Thema: Differenzieren (Ableiten) - Aufgabe zum grafischen Ableiten
Gegeben sei die Funktion f(x) = 2x4+10x3-12x2+5
und deren Graph:
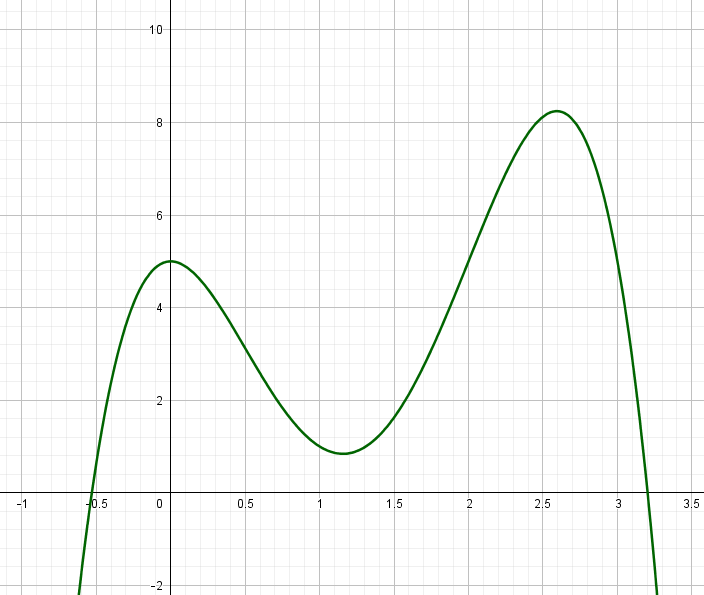
Bestimme grafisch den Graphen der Ableitungsfunktion f ′(x) der Funktion f(x). Eine Skizze des Graphen
von f '(x) reicht aus.
Probiere es erst ohne jeglichen Hinweis. Herauskommen müsste in etwa der folgende skizzierte
Graph:
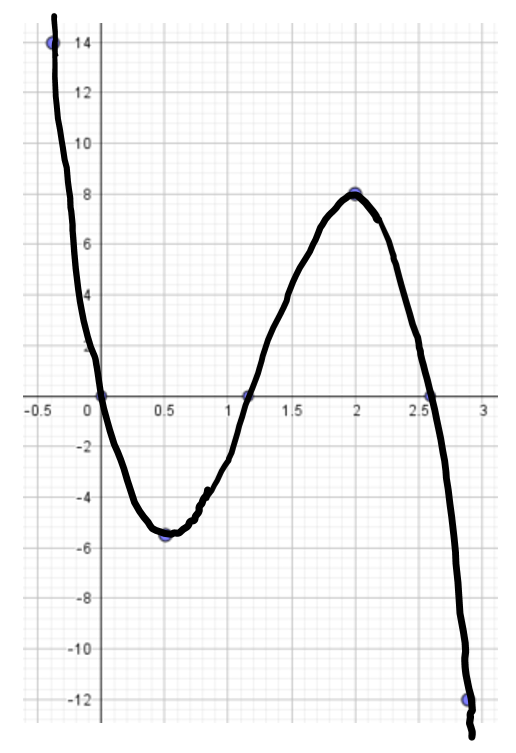
Beim grafischen Ableiten bestimmst Du an verschiedenen Punkten des Graphen von f(x) die Steigung
der Tangente. Diese Steigungen werden dann als Funktionswerte (y-Werte) im Graphen der Ableitungsfunktion f ′(x) eingetragen.
Hinweis 1
Suche Dir zunächst markante Punkte, wie Hoch-, Tief- und Wendepunkte der Funktion f(x) heraus
und bestimme dort mit Hilfe der Tangente und einem Steigungsdreieck die Steigung.
Hinweis 2
Am einfachsten ist das Bestimmen der Steigung an den Hoch- und Tiefpunkten. Denn dort ist die
Steigung immer 0.
Hinweis 3
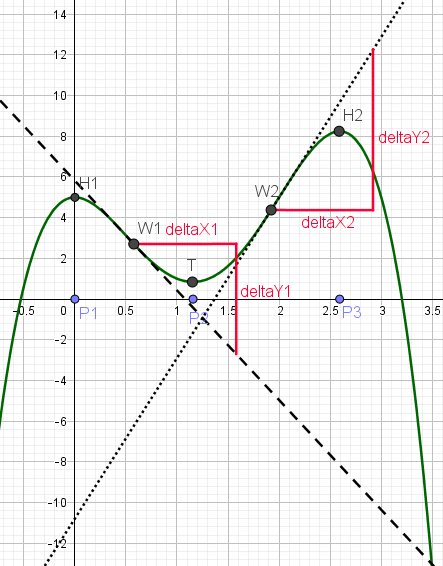
Abgelesene Hochpunkte und Tiefpunkte hat die Funktion ungefähr folgende: H1(0|5) ; T(1,15|0,8) ; H2(2,6|8,2)
Hinweis 4
Das heißt, dass die Funktion f(x) an den Stellen x=0, x=1,15 und x=2,6
die Steigungen f '(0)=0, f '(1,15)=0 und f '(2,6)=0 besitzt.
Hinweis 5
Es werden also die Punkte P1(0|0), P2(1,15|0) und P3(2,6|0) auf der x-Achse des Graphen der Funktion f '(x)
eingetragen.
Hinweis 6
Es ergibt sich zunächst folgendes:
Hinweis 7
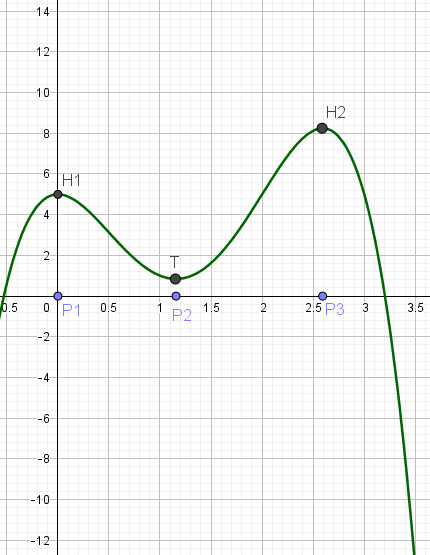
Die Hoch und Tiefpunkte der Funktion f(x) ergeben also die Nullstellen der Funktion f '(x).
Weitere markante Punkte sind die Wendepunkte der Funktion f(x).
Hinweis 8
Abgelesene Wendepunkte hat die Funktion ungefähr folgende: W1(0,6|2,7) ; W2(1,9|4,4)
Hinweis 9
In die Wendepunkte W1(0,6|2,7) ; W2(1,9|4,4) müssen Tangenten gezeichnet werden.
Hinweis 10
Es ergibt sich folgendes:
Hinweis 11
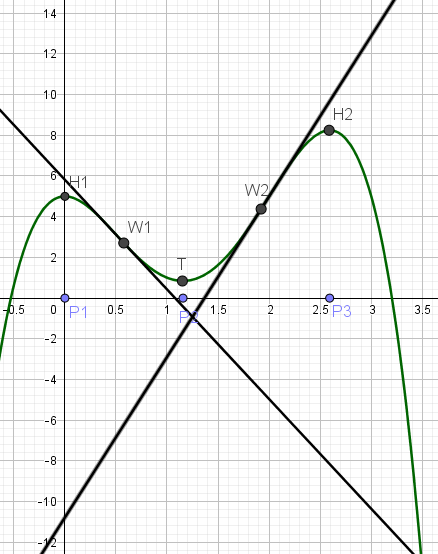
An die Tangenten müssen jetzt jeweils gut ablesbare Steigungsdreiecke gezeichnet werden.
Hinweis 12
Es ergibt sich z.B. folgendes:
Hinweis 13
Steigungsdreiecke können aber im Prinzip irgendwo an die Tangenten gezeichnet werden. Hauptsache die
Seitenlängen der Steigungsdreiecke können gut abgelesen werden.
Jetzt müssen die Seitenlängen der Steigungsdreiecke bestimmt werden.
Hinweis 14
Die Seitenlängen betragen ungefähr:
Hinweis 15
Jetzt müssen mit Hilfe der Seitenlängen der Steigungsdreiecke die Steigungen der Tangenten und damit
die Steigung in den Punkten durch die die Tangenten laufen bestimmt werden.
Hinweis 16
Die Steigung im Wendepunkt W1 beträgt:Hinweis 17
Die Steigung m1 = -5,6 ist negativ, da der Graph von f(x) im Wendepunkt W1 fällt.
Die Steigung im Wendepunkt W2 beträgt:
Die Steigung m2= +7,8 ist positiv, da der Graph von f(x) im Wendepunkt W2 steigt.
Das heißt, dass die Funktion f(x) an den x-Koordinaten der Wendepunkte x=0,6 und x=1,9
die Steigungen f '(0,6) = -5,6 und f '(1,9) = +7,8 besitzt.
Hinweis 18
Es werden also die Punkte P4(0,6|-5,6) und P5(1,9|7,8) des Graphen der Funktion f '(x)
eingetragen.
Hinweis 19
Es ergibt sich jetzt folgendes:
Hinweis 20
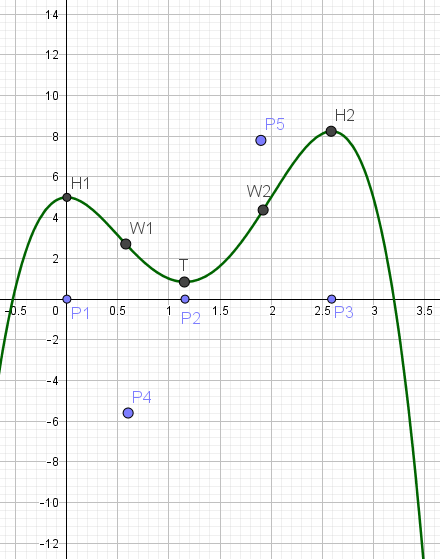
Die Hoch und Tiefpunkte der Funktion f(x) ergeben also die Nullstellen der Funktion f '(x).
Es könnten jetzt noch weitere Steigungswerte der Funktion f(x) links neben dem Hochpunkt H1
und rechts neben dem Hochpunkt H2 bestimmt werden. Da aber eine Skizze reicht und die Steigungswerte
für die markanten Punkte, also die Hoch-, Tief- und Wendepunkte der Funktion f(x) bestimmt wurden, können
die Punkte P1-P5 jetzt miteinander verbunden werden.
Hinweis 21
Abschließend eregibt sich die folgende Skizze der Ableitungsfunktion f '(x) in rot:
Hinweis 22
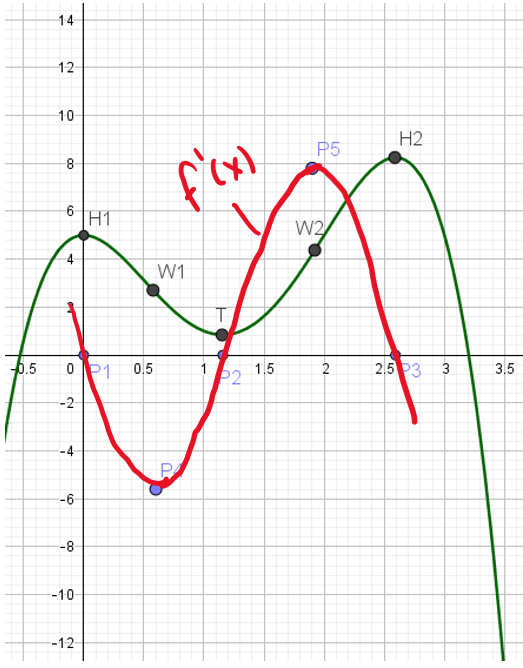
Da die Steigungen in den Wendepunkten die jeweils größten zwischen den Hoch- und Tiefpunkten sind, sind sie
wiederum Tief und der Hochpunkt der Ableitungsfunktion f '(x).
Wenn Du auf die Schaltfläche "Weiter" klickst,
dann geht es mit einer Aufgabe zum grafischen Ableiten weiter.



