Thema: Differenzieren (Ableiten) - Grafisches Ableiten

Der Graph der Ableitungsfunktion f '(x) kann näherungsweise durch das grafische Ableiten der Funktion f(x) bestimmt werden. Dazu muss man für mehrere Punkte des Graphen mit Hilfe der Tangenten, die durch diese Punkte verlaufen, die Steigungen bestimmen. Denn die Tangente an dem Graphen, die durch einen Punkt auf dem Graphen verläuft, ist genau die Steigung des Graphen in diesem Punkt.

Die Steigung eines Graphen an einem bestimmten Punkt wird durch die Steigung der Tangente an den Graphen in genau diesem Punkt definiert.

Eine Tangente ist eine Gerade, die eine Kurve in genau einem Punkt berührt, ohne sie in einer kleinen Umgebung dieses Punktes zu schneiden. Die Tangente gibt die Richtung der Kurve an diesem Berührpunkt wieder. Sie ist somit die Gerade, die den Graphen lokal am besten approximiert (annähert).

In der folgenden Animation kann die Strecke des Wanderers aus dem Beispiel von der voherigen Seite mit Hilfe des Schiebereglers "waagerechte Strecke x" nachgewandert werden. Es wird in jedem Punkt, auf dem sich der Wanderer befindet, die Tangente angezeigt.

In der folgenden Animation wird zusätzlich ein Steigungsdreieck, in den Punkten in denen sich der Wanderer gerade befindet an die zugehörige Tangente gezeichnet. Die Steigungsdreiecke haben alle ein deltaX = 500 Meter.

Um die Ableitungsfunktion grafisch zu erstellen, sucht man sich einige markante Punkte der Funktion heraus. Beginnen wir mit dem Punkt (0|0), an dem der Wanderer seine Wanderung beginnt:


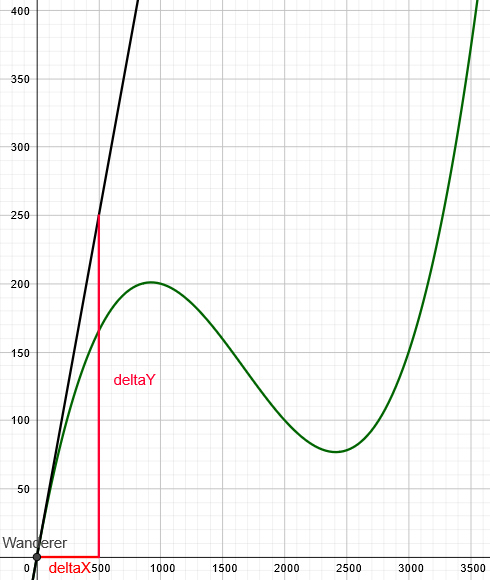
Hier ist die Länge der Strecke deltaX = 500m und die Länge der Strecke deltaY = 250m.

Die Steigung einer Geraden kann mit Hilfe des Steigungsdreiecks bestimmt werden, in dem die Strecke deltaY durch die Strecke deltaX dividiert wird:

$\text{Steigung}=\frac{\mathrm{deltaX}}{\mathrm{deltaY}}$

Das bedeutet, dass die Steigung m der Tangente im Punkt (0|0) folgendermaßen berechnet wird:

$\begin{array}{}\text{m}=\frac{250\text{m}}{500\text{m}}\text{m}=\frac{1}{2}\text{m}=0.5\end{array}$

Die Steigung beträgt der Tangente im Punkt (0|0) beträgt also 0,5.

Als nächster markanter Punkt soll die Steigung der Tangenten durch die Bergspitze im Punkt (800|200) bestimmt werden.



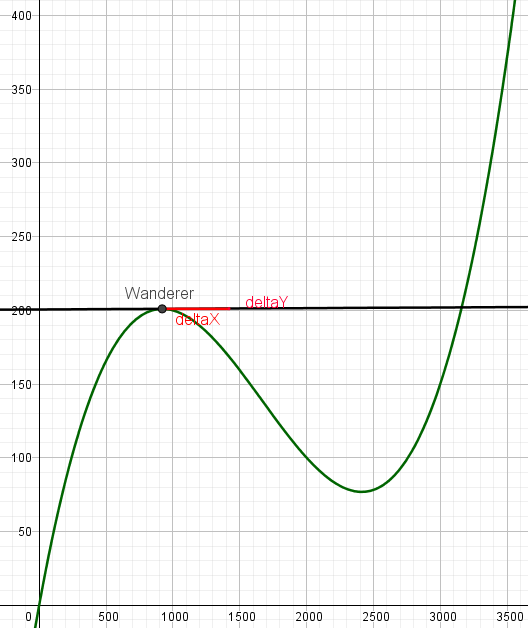
Hier existiert kein echtes Dreieck mehr. Hier ist die Länge der Strecke deltaX = 500m und die Länge der Strecke deltaY = 0m.

Das bedeutet, dass die Steigung m der Tangente im Punkt (800|200) folgendermaßen berechnet wird:

$\begin{array}{}\text{m}=\frac{0\text{m}}{500\text{m}}\text{m}=\frac{0}{500}\text{m}=0.0\end{array}$

Die Steigung beträgt der Tangente im Punkt (800|200) beträgt also 0. Dies ist in jedem Hochpunkt einer Funktion so.

Als nächster markanter Punkt soll die Steigung der Tangenten durch die steilste Stelle zwischen der Bergspitze und dem Talboden bestimmt werden. Dies ist der Wendepunkt bei ca. (1680|140).



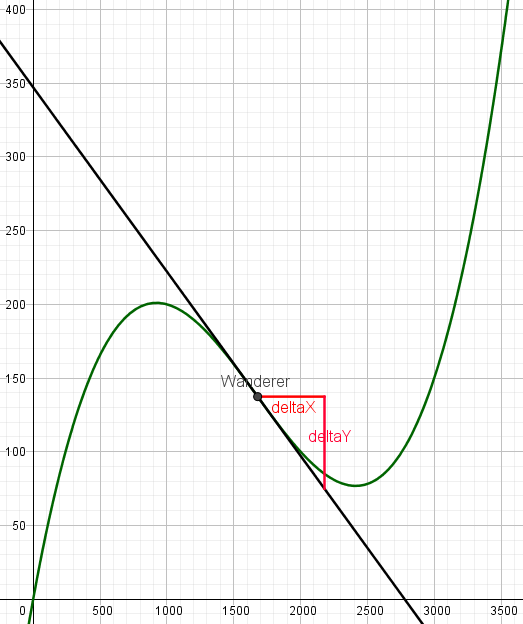
Hier ist die Länge der Strecke deltaX = 500m und die Länge der Strecke deltaY ≈ 138m - 78m = 60m.

Das bedeutet, dass die Steigung m der Tangente im Punkt (1680|140) folgendermaßen berechnet wird:

$\begin{array}{}\text{m}=\frac{-60\text{m}}{500\text{m}}\text{m}=\frac{-60}{500}\text{m}=\frac{-3}{25}\text{m}\approx -0.12\end{array}$

Die Steigung der Tangente im Wendepunkt (1680|140) beträgt also -0.12 und ist zwischendem Hochpunkt und dem Tiefpunkt die größte (negative) Steigung. Die Steigung ist hier negativ, da der Graph um diesen Punkt herum fällt.

Als nächster markanter Punkt soll die Steigung der Tangenten durch den Talboden bestimmt werden. Dies ist der Tiefpunkt bei ca. (2400|78).



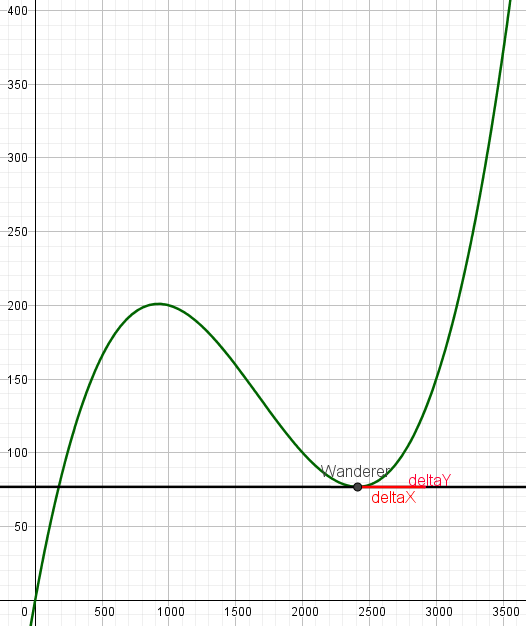
Hier existiert wieder kein echtes Dreieck mehr. Hier ist die Länge der Strecke deltaX = 500m und die Länge der Strecke deltaY = 0m.

Das bedeutet, dass die Steigung m der Tangente im Punkt (2400|78) folgendermaßen berechnet wird:

$\begin{array}{}\text{m}=\frac{0\text{m}}{500\text{m}}\text{m}=\frac{0}{500}\text{m}=0.0\end{array}$

Die Steigung der Tangente im Punkt (2400|78) beträgt also 0. Dies ist in jedem Tiefpunkt einer Funktion so.

Als letzter Punkt soll die Steigung der Tangenten durch Punkt bei ca. (3000|150) bestimmt werden.



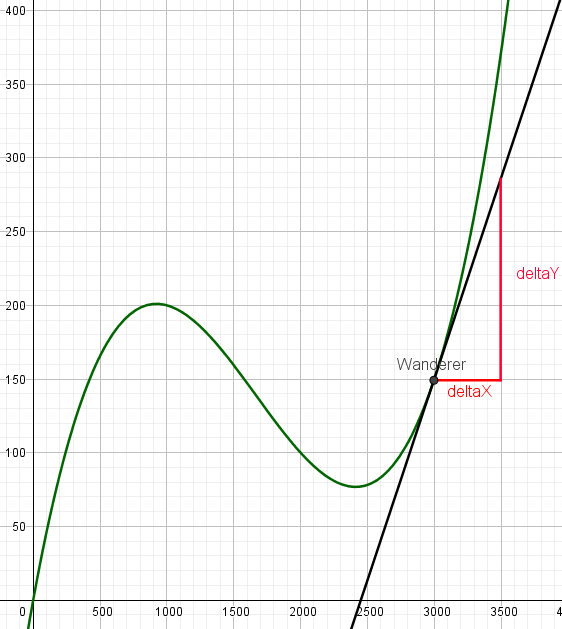
Hier ist die Länge der Strecke deltaX = 500m und die Länge der Strecke deltaY ≈ 285m - 150m = 135m.

Das bedeutet, dass die Steigung m der Tangente im Punkt (3000|150) folgendermaßen berechnet wird:

$\begin{array}{}\text{m}=\frac{135\text{m}}{500\text{m}}\text{m}=\frac{27}{100}\text{m}=0.27\end{array}$

Die Steigung der Tangente im Punkt (3000|150) beträgt also 0,27.

Insgesamt wurden jetzt also exemplarisch für 5 Punkte, darunter der Anfangspunkt, der Hochpunkt, der Wendpunkt und der Tiefpunkt auf ihre Steigungen hin analysiert, die in der folgenden Wertetabelle zusammengefasst werden:

Werden diese Punkte in ein Koordinatensystem eingetragen, dann ergibt sich folgendes Bild:

Jetzt versucht man diese Punkte durch ein Kurve so gut wie möglich zu verbinden und es ergibt sich die grafisch ermittelte Steigungsfunktion:



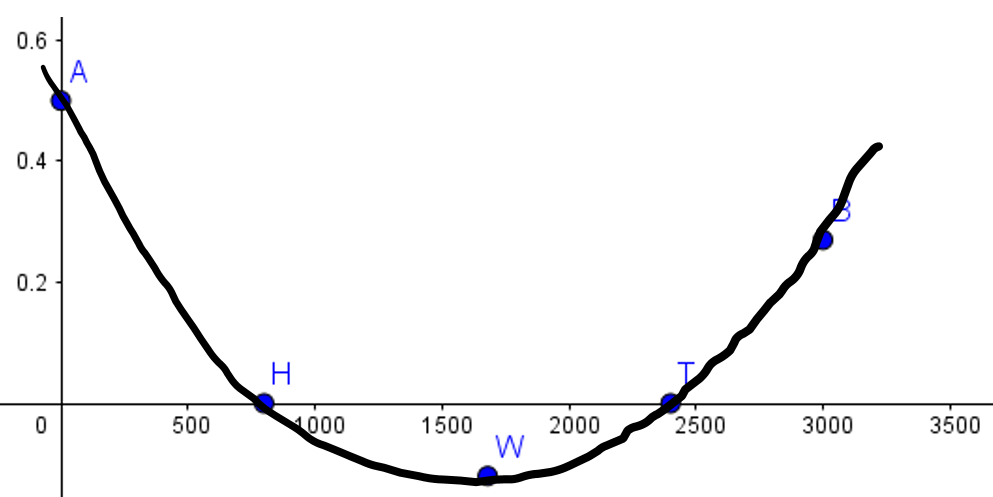
Sollte zu wenige Punkte für ein "schönes" verbinden zur Verfügung stehen müssen noch weitere Zwischenwerte mit Hilfe der zuvor beschriebenen Methode für Steigungen bestimmt werden.

Wenn Du auf die Schaltfläche "Weiter" klickst, dann geht es mit dem formalen Ableiten ganzrationaler Funktionen weiter.