Thema: Differenzieren (Ableiten)

Beim Differenzieren (Ableiten) geht es nicht darum einen durch eine Funktion f beschriebenen Sachverhalt direkt zu untersuchen, sondern das Änderungsverhalten dieser Funktion zu untersuchen.

Beispiel:
Stell dir vor, du gehst einen Weg bergauf und möchtest wissen, wie steil der Weg an einer bestimmten Stelle ist. Der Grad der Steigung (wie stark der Weg ansteigt) hängt davon ab, wie die Höhe des Weges mit der zurückgelegten waagerechten Strecke zusammenhängt.

Höhenkurve: Der Höhenverlauf des Weges lässt sich durch eine Funktion h(x) beschreiben, wobei h die Höhe und x die waagerechte Strecke ist, die du gegangen bist.

Beim Differenzieren erhält man als Ergebnis die Ableitungsfunktion und damit die Steigungsfunktion:
Die Ableitungsfunktion h′(x) (gesprochen h Strich von x) gibt die Steigung des Weges an, also wie stark sich die Höhe z.B. pro gelaufenem waagerechten Meter ändert. An einem steilen Abschnitt ist die Steigung größer, an flachen Abschnitten ist sie kleiner. Wenn du wissen willst, wie steil es an einer bestimmten Stelle x ist, schaust du dir den Wert der Ableitungsfunktion h'(x) an dieser Stelle an.

Verallgemeinert lässt sich sagen, dass die Ableitungsfunktion f '(x) die Änderung der Funktion f(x) beschreibt. So kann beispielsweise die x-Koordinate die Zeit in Stunden h beschreiben und die dazu gehörigen Funktionswerte f(x) beschreiben den in dieser Zeit zurückgelegten Weg eines Autos in km auf einer Straße. Die Ableitungsfunktion f '(x) beschreibt dann die Änderung des zurückgelegten Weges in km pro gefahrener Stunde. Die Steigung der Funktion f(x) ist dann also die Geschwindigkeit des Autos.

Oder: Die x-Koordinate ist die Menge eines Produktes in Stück. Die dazugehörigen Funktionswerte f(x) beschreiben die dabei entstehenden Gesamtkosten in Euro. Die Ableitungsfunktion f '(x) beschreibt dann die Änderung der Gesamtkosten in Euro pro produziertem Stück des Produktes. Die Steigung der Funktion f(x) sind dann also die Stückkosten der Produktion.
Es ließen sich viele weitere Beispiele angeben, bei denen solche Änderungen mathematisch beschrieben werden müssen. Deshalb ist das Differenzieren (Ableiten) ein wichtiges praxisrelavantes Gebiet der Mathematik.

Die folgende Abbildung soll den Begriff der Steigung noch einmal veranschaulichen. Sowohl die waagerechte Strecke x als auch die Höhe h(x) werden in Metern angegeben.

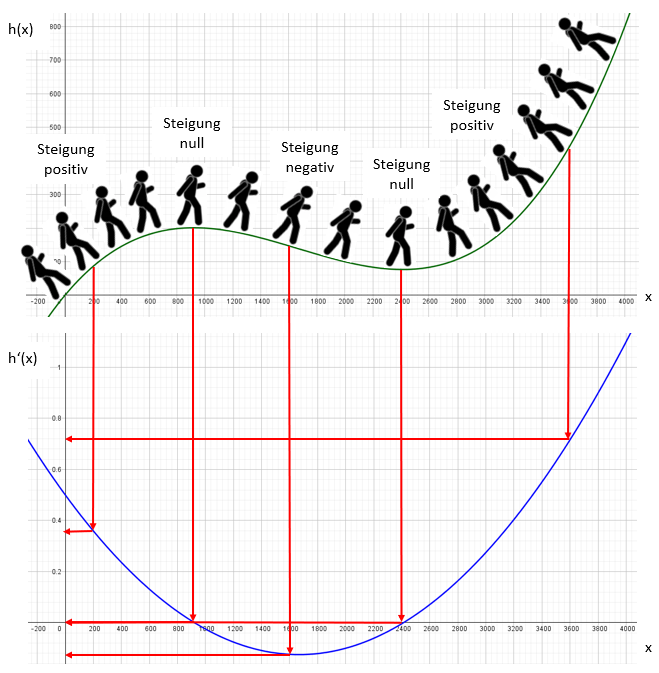
Zu Beginn des Berges bei 0 Metern ist die Steigung positiv und relativ steil.

Bei 200 Metern ist die Steigung immer noch positiv, aber nicht mehr ganz so steil, der zugehörige Steigungswert, der in dem Graphen von h'(x) auf der "y-Achse" abgelesen werden kann, beträgt ca. +0,36. Das bedeutet, dass man an dieser Stelle (würde die Steigung so bleiben) pro gelaufenem waagerechten Meter 0,36 Meter an Höhe gewinnt.

Jetzt wird die Steigung immer geringer, bleibt aber positiv, bis bei ca. 920 Metern die Steigung 0 wird. Der Wanderer hat die Bergspitze (den höchsten Punkt) erreicht. Der Funktionswert h'(920) ist also 0. Das bedeutet, dass man an dieser Stelle (würde die Steigung so bleiben) pro gelaufenem waagerechten Meter nicht mehr weiter an Höhe gewinnt, sondern waagerecht zur x-Achse weiterlaufen würde.

Nach den 920 Metern geht es aber nicht waagerecht zur x-Achse weiter, sondern der Weg geht jetzt den Berg hinunter ins Tal Der Berg fällt also ab. Dies drückt sich jetzt durch eine negative Steigung aus. Dabei ist das Gefälle (die negative Steigung) erst gering und wird dann bei ca. 1600 Metern am steilsten. Hier beträgt das Gefälle ca. h'(1600) = -0,12. Das bedeutet, dass man an dieser Stelle (würde die Steigung so bleiben) pro gelaufenem waagerechten Meter 0,12 Meter an Höhe verliert.

Der Wanderer läuft weiter und es wird immer flacher. Nach ca. 2400 Metern hat er den Tiefpunkt des Tales erreicht. Der Funktionswert h'(2400) ist 0. Das bedeutet, dass der Wanderer an dieser Stelle (würde die Steigung so bleiben) pro gelaufenem waagerechten Meter nicht mehr weiter runter läuft, sondern waagerecht zur x-Achse weiterlaufen würde.

Nach den 2400 Metern geht es aber nicht waagerecht zur x-Achse weiter, sondern der Weg geht jetzt wieder den Berg hinauf. Der Berg steigt also wieder an. Dies drückt sich jetzt wieder durch eine positive Steigung aus. Dabei ist die Steigung erst gering und wird dann immer steiler. Bei ca. 3600 Metern beträgt die Steigung ca. h'(3600) = +0,72. Das bedeutet, dass man an dieser Stelle (würde die Steigung so bleiben) pro gelaufenem waagerechten Meter 0,72 Meter an Höhe gewinnt. Die Steigung der Funktion h(x) wird mit der Ableitungsfunktion h'(x) direkt beschreiben und drückt also hier im Beispiel die Änderung der Höhe in Abhängigkeit von der zurückgelegten (waagerechten) Strecke x aus.

Wenn Du auf die Schaltfläche "Weiter" klickst, dann geht es mit dem graphischen Ableiten weiter.